‘Zonder statistiek is het onwaarschijnlijk dat je je beste product-performance vindt en consistent behoudt’

Toen Wendy Luiten leerde programmeren, gebruikte ze ponskaarten die in gigantische computers werden ingevoerd. Tegenwoordig kan ze de meest complexe berekeningen en ontwerpsimulaties met een druk op de knop maken op haar laptop. Tijdens Luitens carrière was ze getuige van een ongekende toename in rekenkracht en rekenmogelijkheden. Nadat ze in 1984 afstudeerde aan de Universiteit Twente, begon ze aan een indrukwekkende carrière als thermisch expert en als Six Sigma Master Black Belt bij Philips. Tegenwoordig werkt ze als consultant.

Die ervaring gaf haar een betere kijk op statistiek en gebruik van computersimulaties dan de meeste ingenieurs. Nieuwe software biedt geweldige mogelijkheden voor het maken van ontwerpsimulaties en digital twins. Maar met het ogenschijnlijke gemak van deze nieuwe methoden vergeet je gemakkelijk dat een simulatie niet de werkelijkheid is. Een simulatiemodel moet gevalideerd worden om er zeker van te zijn dat de berekeningen echt kloppen en dat alle effecten zijn meegenomen. Bovendien beschrijven simulaties een ideale wereld, zonder variatie. In de werkelijke wereld kunnen toleranties en variaties in gebruik ervoor zorgen dat het product niet altijd doet wat ervan verwacht wordt, en dat leidt tot teleurstelling.

‘Sommige mensen doen hun metingen maar één keer, zonder herhaling’, zegt Luiten. 'Op basis daarvan beslissen ze of het ontwerp wel of niet goed is. Dat is riskant. Je weet niet hoe goed de meting is, je hebt geen idee van de meetfout, je weet niet hoe representatief het prototype is, je weet niet hoe representatief de usecase is.’

Mensen hebben de neiging om erg optimistisch te zijn over hun meetfout, constateert ze. ‘Ik heb gevallen gezien waarbij mensen dachten dat hun meetfout in de tienden van een graad zat, maar bij een herhalingsmeting bleek het verschil 10 graden C te zijn. In de thermische wereld is dat een ontzettend groot verschil. Als je herhalingsmeting zo'n groot verschil laat zien, kun je er echt niet zeker van zijn dat die meetopstelling een voldoende betrouwbare meting geeft en moet je dat uitzoeken. Maar als je nooit een meting herhaalt, kun je niet weten of de opstelling goed is.

Daarom start Luiten haar nieuwe training Applied statistics for R&D aan High Tech Institute met meetstatistiek. In deze cursus gaat ze dieper in op belangrijke statistische tools die hun waarde hebben bewezen in haar meer dan dertig jaar r&d-ervaring in de industrie. ‘Eerst moet je zien hoe goed je metingen zijn’, legt ze uit. ‘Vervolgens moet je de steekproefgrootte kunnen schatten, het aantal metingen dat je nodig hebt om een bepaald effect met voldoende waarschijnlijkheid aan te tonen. Zodra je voldoende accuraat en precies meet, kun je verschillende productconfiguraties onderzoeken en de beste kiezen. Tot slot kijk je naar het gemiddelde en de spreiding van de productfunctie, en uiteindelijk heb je succes en is er een product dat doet wat het moet doen en consistent aan de verachtingen voldoet.

Toevallige meetfout

Luiten merkt op dat ingenieurs zich vaak bewust zijn van de systematische meetfout, maar niet van de toevallige fout. ‘Systematische fouten zijn heel bekend’, zegt ze. ‘Je kunt een golden sample meten en de resultaten corrigeren, dat is een de facto kalibratie van je meting. Dat is een bekende procedure en onderdeel van veel practica in het hoger onderwijs.’

‘De meeste mensen houden echter geen rekening met de toevallige fout of gebruiken blindelings een standaardwaarde van 1, 5 of 10%. Maar in werkelijkheid hangt de toevallige fout af van het meetinstrument en ook van wie de metingen uitvoert. De statistische methode om de toevallige fout te achterhalen is meestal geen onderdeel van het practicum, dus dit is niet zo bekend en wordt minder vaak gedaan. Maar de eerste keer dat dat gebeurt is de uitkomst vaak verrassend.’

Luiten noemt een aantal gevallen waar ze zelf mee te maken heeft gehad. ‘Ik heb gevallen gezien waarin mensen ervan overtuigd waren dat ze bijna geen toevallige fout hadden, omdat ze een hele dure geautomatiseerde meetmachine hadden. Maar het bleek dat de operators het meetsample op een andere manier maakten en dat veroorzaakte een grote toevallige fout. In een ander geval claimden verschillende ontwikkelingslaboratoria allemaal een meetfout van 5% - maar toen ze een doosje producten rondstuurden in een round-robin-test, was er een verschil van een factor 2, vanwege verschillen in de meetopstelling waarvan ze dachten dat die er niet toe deden. Ik heb gezien dat schijnbare schommelingen in productkwaliteit konden worden gekoppeld aan de operator die de metingen uitvoerde. In alle gevallen waren mensen er absoluut van overtuigd dat ze een verwaarloosbare toevallige fout in de metingen hadden, want deze resultaten waren totaal onverwacht. Maar je weet alleen hoe groot de toevallige fout is en waar die vandaan komt als je het test.’

Herhaalmetingen

De toevallige meetfout is vooral belangrijk als het gaat om zogenaamde statistical power - de kans dat je een specifiek effect meet als het er is. Als het effect dat je wilt meten ongeveer even groot is als je meetfout en je herhaalt je meting twee keer, dan is de kans dat je dat effect bewijst veel kleiner dan je denkt, kleiner dan 10%. Luiten: ‘Dus, als een verandering in het ontwerp je een 5C lagere temperatuur oplevert, en je willekeurige meetfout is 5C, dan zul je dat in 1 op de 10 metingen zien, en gemiddeld 9 op de 10 keer komt het er niet uit, zelfs als je de meting in tweevoud doet. Als je de power wilt verbeteren, moet je of de meetfout verlagen, of meer herhalingsmetingen doen zodat je een voldoende steekproefgrootte hebt.’

Soms zien mensen herhalingsmetingen als overbodig en verspilde moeite, maar daar is Luiten het niet mee eens. ‘De echte verspilling is het uitvoeren van experimenten met een te lage power, want als je naderhand geen conclusie kan trekken, zijn alle kosten en moeite van het experiment weggegooid geld.’

Testen van verschillende ontwerpconfiguraties

Naast meetfouten en het schatten van de steekproefgrootte is het onderzoeken van verschillende ontwerpconfiguraties een belangrijk onderdeel van de cursus. Je kunt dat in hardware doen, maar dat is misschien niet de meest effectieve optie. ‘Tegenwoordig kun je veel virtueel testen’, zegt Luiten.’ Voordat je een prototype maakt, kun je al experimenteren met behulp van computersimulaties. De input kan variëren van materialen en afmetingen tot hoe je meet en regelt. Je kunt bijvoorbeeld het effect van verschillende materialen of afmetingen modelleren, of het gebruik van een andere mechanische lay-out, of verschillende instellingen in een besturingsalgoritme. Er zijn heel veel keuzes, zowel in de architectuur als in de implementatie. Je wilt uitzoeken welke inputs er echt toe doen en wat voor invloed ze hebben, want je wilt niet naderhand erachter komen dat een eerdere beslissing verkeerd was.’

Een trial-and-error-aanpak is vaak te duur en tijdrovend. De statistische benadering bestaat uit het opzetten van een reeks experimenten op een specifieke manier, waarbij meerdere inputs tegelijkertijd worden gevarieerd. Je vergelijkt in de analyse dan niet twee experimenten met elkaar, maar twee groepen, om het effect van een enkele input of van interacties te bepalen.

Luiten: ‘Dit is een heel krachtige aanpak, vooral in combinatie met computersimulaties, maar voor een klein aantal inputs kun je dit ook in hardware doen. Als je de experimenten in hardware uitvoert, bepaalt de berekende steekproefgrootte uit de eerdere fase het aantal herhalingen voor de verschillende experimenten. Als de experimenten virtueel worden uitgevoerd, door middel van computersimulaties, dan wordt de steekproefgrootte gebruikt voor de validatie-experimenten voor het computermodel.’

De oplossingsruimte in kaart brengen

Statistische methoden helpen om alle mogelijke configuraties die samen de oplossingsruimte vormen in kaart te brengen en de beste te vinden. Luiten: ‘Je bereikt je optimale keuze niet toevallig. Als je twee inputs hebt in een laag-hoog range heb je vier mogelijkheden. Maar als je er vijf hebt dan zijn het er al 32. En de meeste productontwerpen hebben er meer dan vijf. En dan hebben we het nog niet eens over alle mogelijke toleranties en alle verschillende gebruikers en toepassingen. Zonder een structurele, op statistiek gebaseerde aanpak is de kans klein dat je de optimale consistente performance vindt.’

De beste keuze maken

Het volgende gereedschap in de statistische gereedschapskist is optimalisatie, het maken van de beste keuze. Als je eenmaal hebt ontdekt welke inputs er echt toe doen en hoe ze uitwerken, dan kun je een onderbouwde keuze maken die het beste bij je doel past. Vaak zijn er meerdere factoren die meespelen, bijvoorbeeld als je een hoge sterkte wilt maar tegelijkertijd een laag gewicht. Multiple Response Optimization is hiervoor een bekende methode.

Het effect van input-toleranties

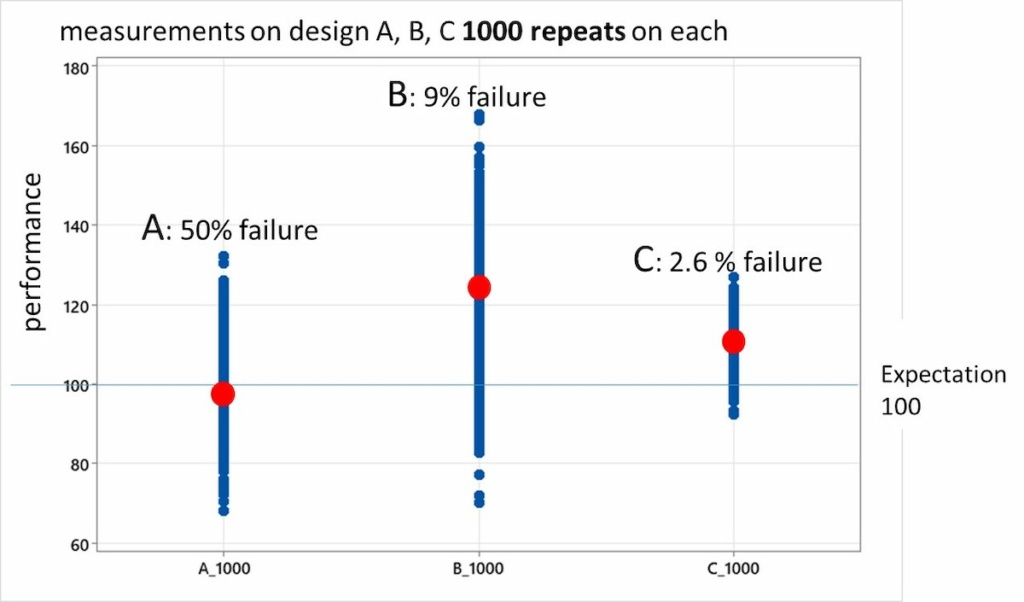
‘Als je eenmaal weet wat het effect van een input is, is het ook belangrijk om naar de tolerantie te kijken, en wat voor variatie die weer veroorzaakt in je output’, vervolgt Luiten. ‘Dit is ook iets waar mensen minder bekend mee zijn, maar als je eenmaal weet hoe je dit moet doen is het niet echt moeilijk. En het is belangrijk. Om een ontwerp tot een succes te maken, gaat het niet alleen om piekprestaties, maar ook om consistentie. Met behulp van statistische simulaties kun je een statistisch model maken om het gemiddelde en de variatie van je output te koppelen aan de statistische verdeling van je input.’

Mensen zeggen soms dat dit zinloos is omdat de input-variatie toch niet bekend is. Maar als een input belangrijk is, dan is het riskant om geen rekening te houden met de variatie, want dan heb je geen borging voor consistente productkwaliteit. Als het statistische model laat zien dat de input belangrijk is, heb je een goede reden om met de leverancier in gesprek te gaan en ernaar te vragen. In de auto-industrie is het bijvoorbeeld zo ingeburgerd dat er formele procedures afgesproken zijn die vastleggen hoe groot de standaarddeviatie mag zijn.

Autorijden

Luitens cursus presenteert de onderdelen in samenhang, het is een keten. Als je bijvoorbeeld simulatieresultaten wilt valideren, dan heb je ook meetstatistiek nodig die je vertelt wat je toevallige fout is. Dit laat op zijn beurt zien hoe groot je steekproef moet zijn, zodat de experimentele opzet voldoende power heeft. ‘Pas dan kun je beslissen of je je validatie kunt vertrouwen’, zegt Luiten.

Ze heeft een pragmatische benadering. Voor haar is statistiek een toegepaste vaardigheid, een middel om een doel te bereiken. Statistiek wordt op de universiteit heel theoretisch onderwezen’, zegt Luiten. ‘Ik zag dit bij mijn eigen studie, en ik zag het toen mijn kinderen studeerden. Het wordt onderwezen op een manier die in mijn werk maar heel beperkt bruikbaar was. Ik vergelijk het met autorijden: je hoeft niet te weten hoe de motor werkt om van A naar B te rijden. Het doel van de cursus is niet om een statistisch expert te worden, maar om statistiek toe te passen om je doel te bereiken.’ En Excel en statistieksoftware maken de toepassing tegenwoordig veel toegankelijker.

Six Sigma Master Black Belt

Luiten is een Master Black Belt in Design for Six Sigma, en haar carrière heeft haar een diep inzicht in en een rijke ervaring met de toepassing van statistiek in innovatieprocessen opgeleverd. ‘Mijn ervaring is dat veel ingenieurs leren door te doen, en dat is logisch. Je kunt niet leren zwemmen door naar de Olympische Spelen te kijken, je moet zelf het water in, al is het maar om te leren drijven. Dus hebben we oefeningen, in Excel of in een speciale statistiektool.’ Voor Luiten is statistiek een waardevol gereedschap voor mensen, breed toepasbaar van technische experts tot ontwerpers en teamleiders tot systeemarchitecten.

‘Dit is een toepassingsgerichte cursus voor mensen in innovatie, mensen die producten ontwikkelen en onderzoek doen. Als je output meet in continue numerieke parameters, maakt het niet uit in welk technisch vakgebied je werkt. Ik heb deze technieken gebruikt in thermische toepassingen, maar het is gewoon wiskunde, je kunt die in elk vakgebied toepassen van mechanica en elektronica tot optica en zelfs software. Hoe je de wiskunde toepast, leer je in de cursus; waarvoor je dat doet, maak je zelf uit.’